MARATHON číslo 63 ( z/2005 )
Proč se zabýváme binárním maticovým modelem pojmu? Připomeňme si - v oblasti spontánního myšlení lze identifikovat mj. dva elementární procesy:
* Spojení pojmů do pojmových určení (vytváření kombinací pojmových určení).
* Hledání interpretace pojmových určení (spojování pojmových určení se strukturovanou zásobou představ).
(Základních funkcí našeho spontánního pojmového myšlení je nepochybně více, zejména schopnost "ozvat se" - viz dále fenomén relevantního přesahu.)
Binární maticový model pojmového poznání nám dá využitelnou představu o tom, jak probíhá naše pojmové myšlení, včetně procesů probíhajících spontánně a včetně jejich vzájemné interakce.
Tato představa je velmi důležitá pro vycvičení našeho spontánního myšlení, zejména v následujících dvou směrech:
* Pokud víme, jaké operace v oblasti našeho spontánního myšlení probíhají, pokud si dovedeme představit, jakou mají podobu, víme, na co se zaměřit, a tím dochází ke kultivaci našeho spontánního myšlení.
* Pomocí modelu dokážeme rozpoznat některé standardní situace, popsat jejich strukturu (jde zejména o problém přesahu stávajícího poznání); na základě toho se pak můžeme orientovat na to nejpodstatnější.
Poznámka:
Binární maticový model pojmového poznání je jen a jen modelem. Je přibližným a spíše povrchním vyjádření toho, jak procesy našeho myšlení probíhají:
* Rozdíl je již v tom, že naše myšlení má spíše analogový charakter. To ovšem není tak významné. Analogový záznam hudby (gramofonová deska) se zase tak moc neliší od digitálního (CD).
* Podstatnější je to, že procesy našeho myšlení jsou složitější než to, co je schopen náš model zachytit. Ale ani to není principiální nedostatek - až se aplikací modelu dojde k tomu, že v něčem nevyhovuje, bude možné jej zobecnit.
Není žádné umění říci, že "něco je mnohem složitější". Mnohem obtížnější je ukázat "v čem je to složitější". Náš binární maticový model posouvá představu o procesech v našem myšlení podstatně dál, než modely využívající jen výrokovou logiku (i když binární model je založen na respektování výrokové logiky).
Začněme tím základním: Co je pojem a pojmové určení?
Vezměme si pojem "václavka" a "kapitál", návazně na to pak spojení pojmů "Václavka je jedlá." a "Kapitál vzniká odložením spotřeby.".
* Umíme si představit, jak vypadá struktura pojmu?
* V jaké podobě existuje předmět pojmu?
* Jak spolu jednotlivé pojmy souvisejí?
* K čemu nám pojmové vyjádření reality je?
* Jakým způsobem jej využíváme?
* Můžeme testovat schopnost vyjádřit realitu prostřednictvím pojmů?
* Můžeme se v této schopnosti cvičit?
Při studování následujícího textu je dobré znát základy výrokové logiky. Co dokáže a co nedokáže výroková logika? Připomeňme si - výroková logika používá logické spojky jako Ø (negace), È (konjunkce), Ç (disjunkce), Û (ekvivalence), Þ (implikace) a pojmy jako axiomy, předpoklady, odvození, důkaz.
Podle výrokové logiky "chodí" počítače..., "chodí" podle ní také naše myšlení? Pokud ano, tak proč nám nepomáhá její znalost? Pokud ne, tak v čem ji naše myšlení přesahuje?
(Platí ovšem: Naše myšlení nesmí pravidla výrokové logiky porušit.)
Jedním z důvodů. proč nevystačíme s výrokovou logickou je samotná realita, o které naše myšlení pojednává. A ta je odlišná, než předpokládá výroková logika. Podle ní:
* Předmět pojmu = to, co je daným pojmem vyjádřeno.
* Existuje následující jedno-jednoznačná korespondence mezi pojmem a předmětem pojmu.
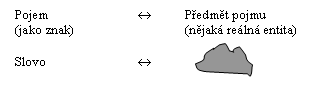
Tam, kde můžeme realitu převést do podoby izolovaných entit, tam "zafunguje" výroková logika. Existuje ovšem v realitě (jakkoli pojaté) něco, co je entitou ("jsoucnem o sobě") a jako takové je předmětem pojmu? Nikoli. Platí následující:
* V realitě neexistují "entity" jako "jsoucna o sobě".
* Naše představa o předmětu je určitý koncept (může se měnit)
* Ten si vytváříme každý sám (má individuální rozměr).
* Existuje v něm určitá shoda mezi lidmi, ale ne absolutní (konvence, výklad práva).
* Neexistuje předmět jednoho pojmu, ale jen jejich celého systému.
* Tímto předmětem je realita samotná.
* Pojmovými určeními vytváříme a dotváříme představu o předmětu pojmu.
* Představa o předmětu pojmu závisí na vzájemných pojmových určeních.
* Představa o předmětu pojmu se mění, vyvíjí.
(Z tohoto pojetí budeme vycházet v našem přístupu.)
Vymezení pojmového poznání:
* Pojmové poznání se sestává (z pojmů a pojmových určení).
* Pojmové určení je vyjádření jednoho pojmu jinými pojmy.
* Pojmové poznání je vyjádření reality tím, že jedny pojmy vyjadřujeme prostřednictvím jiných pojmů.
(Např.: "Václavka je hnědá houba se žábrami, která roste v trsech na pařezech na podzim.")
Rozvíjením pojmových určení dochází i k tvorbě a restrukturaci představ o předmětu jednotlivých pojmů (toho, co si pod jednotlivými pojmy představujeme).
Pojmové určení:
Příkladem pojmového určení je výrok:
"Václavka je jedlá."
Schématicky by bylo možné vyjádřit tento výrok následujícím způsobem:
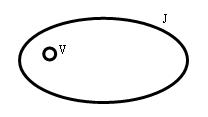
Kde:
V - znamená "být václavkou" (množina václavek)
J - znamená "být jedlý" (množina jedlých věcí)
Taktéž: V Þ J či V É J
Určení typu "václavka je jedlá"
lze přepsat takto:
VJ
00
01
10 neinterpretovatelná
alternativa
11
kde - V je "být václavkou", J je "být jedlý" (0 ne, 1 ano)
- s využitím dvojkového zápisu jsou prezentovány všechny možnosti,
- přeškrtnuta je ta, která je v daném kontextu neinterpretovatelná, vyloučena.
Jiný příklad pojmového určení:
"kapitál je zhodnocující se hodnota"
KH
00
01 neinterpretovatelná
alternativa
10 neinterpretovatelná
alternativa
11
Zde se jedná o určení typu: K Û H
Proč tento těžkopádný způsob prezentace? Tato otázka nás přivádí k myšlence vyjádřit (modelovat) pojmové poznání prostřednictvím binární matice.
Základní myšlenka binární matice
Představme si nyní, že naše pojmové myšlení obsahuje n pojmů.
Pak možných kombinací hodnot je 2n, každé odpovídá jeden řádek binární matice
Možných kombinací neinterpretovatelných řádků (každý neinterpretovatelný řádek je přeškrtnut) je ještě mnohem více, totiž (2n)2.
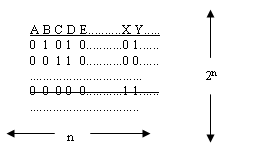
Jaký smysl má binární matice? K čemu ji lze použít?
Binární matice představuje všechny možné kombinace pojmových určení a kombinace případů, kdy mají či nemají interpretaci. Těchto kombinací je ovšem tak obrovské množství,
že nemohou existovat (ve smyslu nějakého záznamu) ani být všechny odzkoušeny (ve smyslu toho, zda jim něco odpovídá či ne). Binární matici však přesto lze chápat jako určitý prostor, v němž lze vyjádřit určité podstatné charakteristiky procesů pojmového myšlení. Neboli - vše, s čím se v myšlení setkáváme, se můžeme pokusit vyjádřit jako jev, k němuž dochází v rámci struktury definované binární maticí. (A pokud bychom narazili na něco, co takto interpretovat nelze, museli bychom model zobecnit.)
Poznámka:
Nepochybně se vyskytne námitka: Myšlení je příliš složité, než aby ho bylo možné vyjádřit něčím tak jednoduchým, jako je - byť i velmi velká - binární matice. Takovou obecnou námitku lze vznést vždy. Mnohem obtížnější je přesně ukázat, v čem je naše myšlení složitější, než aby bylo možné k jeho vyjádření použít náš model.
Poznámka:
Nic nového pod Sluncem. Binární maticový model po formální stránce není nic jiného než představení pojmových určení (výroků ve smyslu výrokové logiky) v podobě úplné normální konjunktivní formy s využitím trochu jiné symboliky. Pro nás má hlavní význam to, že se s touto podobou dá názorně pracovat.
Tyto procesy spojené s pojmovým myšlením probíhají v oblastech, které můžeme považovat za submatice (části) naší výchozí binární matice.
Názorná představa našeho myšlení pomocí binární matice:
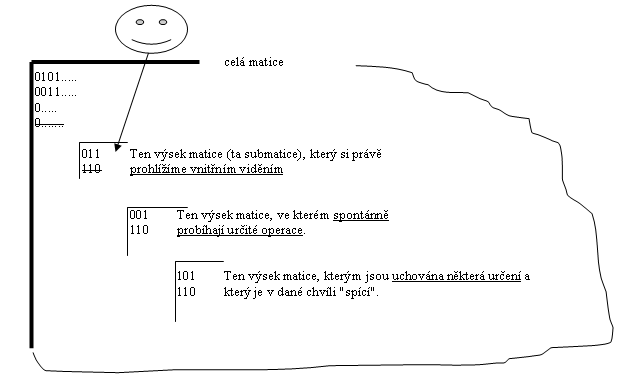
Zaměření pozornosti na určité pojmy můžeme v naší matici chápat jako přehození sloupců do jednoho z rohů v matici. Takový výsek matice, resp. příslušná submatice, se pak stává procesorem-ohniskem, ve kterém spontánně probíhají procesy tvorby a interpretace pojmových určení. Za operaci, která probíhá spontánně můžeme považovat i "zvýznamňování" určitých pojmů, tj. zaměření pozornosti na jejich určitou skupinu a postupně přiřazování dalších. Tomu pak odpovídá jak přesun sloupců, tak i řádků v našem modelovém vyjádření.
Příklad rozboru textu s využitím binárního maticového zápisu
Jako příklad si vezměme následující text, který je z jedné bakalářské práce:
"Stárnutí obyvatelstva je celosvětovým problémem. Nevyhne se vyspělým ekonomickým zemím ani zemím rozvojovým, jako je Česká republika, která za poslední desetiletí prochází značnou ekonomickou, politickou a sociální transformací. Došlo k významným změnám ve věkové struktuře obyvatelstva, v jeho chování a přizpůsobování. Nemalou měrou ke všemu působí technický, vědecký a technologický pokrok, který stále rychleji míří vpřed ve všech oblastech poznání.
S rychle se rozvíjející stárnoucí populací rostou i náklady na důchody, které budou ukrajovat ze státního rozpočtu stále větší část. Oproti roku 1990 se rodí o třetinu méně novorozenců a i to ukazuje naléhavost otázky důchodových reforem. Teprve v posledním roce se populační pokles zastavil. Než tato generace doroste do pracovního věku, aby mohla odvádět peníze na sociální zabezpečení, bude trvat nejméně 20 až 24 let. Po tuto dobu bude muset státní rozpočet obětovat větší sumu peněz na důchody. Také to bude znamenat, že zmenšující se počet pracovně aktivních lidí bude financovat narůstající počet důchodců.
A právě to je klíčový moment, který je cílem této práce. Ukázat, jaký je stávající důchodový systém neudržitelný v důsledku demografického vývoje."
Každou větu lze přepsat ve standardní podobě binárního maticového zápisu. Např. větu "Stárnutí obyvatelstva je celosvětovým problémem." můžeme rozdělit na dvě části:
* stárnutí obyvatelstva - označme So
* celosvětový problém - označme Cp
Výše uvedený výrok "Stárnutí obyvatelstva je celosvětovým problémem." můžeme vyjádřit následující maticí:
SoCp
0 0
0 1
1 0 Tato
kombinace je v daném výroku neinterpretovatelná.
1 1
Vezměme řádek po řádku:
* 00 - Nepochybně existuje něco, co není stárnutím obyvatelstva a co není celosvětovým problémem (00 v prvním řádku je nezajímavý případ, který má v případě spojení jakýchkoli dvou pojmů vždy interpretaci).
* 01 - Existuje něco, co není stárnutím obyvatelstva a současně je celosvětovým problémem.
* 10 - Na vyloučení interpretace tohoto případu
je postavena určitost celé věty. Říká se zde, že nikde na světě není země,
která by si s daným problémem úspěšně poradila a tudíž by pro ni stárnutí
obyvatelstva problémem nebylo. V současné době bychom asi opravdu takovou zemi
těžko hledali.
* 11 - Stárnutí obyvatelstva skutečně je celosvětový problém.
Úkol:
Zkuste takto přepsat a rozebrat některou z dalších vět, resp. jejich částí, např. "Česká republika, která za poslední desetiletí prochází značnou ekonomickou, politickou a sociální transformací.
Nyní se věnujeme rozboru těch vět, které jsou z hlediska rozhodnutí o interpretovatelnosti či neinterpretovatelnosti toho, co tvoří jejich určitost, významné. Vezměme například větu:
"S rychle se rozvíjející stárnoucí populací rostou i náklady na důchody, které budou ukrajovat ze státního rozpočtu stále větší část." Opět ji rozdělme vhodným způsobem na dvě části:
* "s rychle se rozvíjející stárnoucí populací" = totéž jako "narůstá podíl stárnoucí populace", což můžeme označit např. Sp.
* "rostou i náklady na důchody, které budou ukrajovat ze státního rozpočtu stále větší část", což můžeme označit např. Rn.
Výše uvedený výrok "S rychle se rozvíjející stárnoucí populací rostou i náklady na důchody, které budou ukrajovat ze státního rozpočtu stále větší část." můžeme vyjádřit následující binární maticí:
SpRn
0 0
0 1
1 0 Tato
kombinace je v daném výroku neinterpretovatelná.
1 1
Neinterpretovatelnou kombinací zde je případ, kdy narůstá podíl stárnoucí populace, ale nerostou náklady na důchody ve smyslu zvyšování jejich podílu na státním rozpočtu. Jenže to je již velmi sporné tvrzení. Lze ukázat řadu významných interpretací:
* Parametrické úpravy, které by stabilizovaly podíl výdajů ze státního rozpočtu na důchody.
* Hrazení důchodů z jiných zdrojů (fondů) než je státní rozpočet.
* (A zejména:)Prodloužení období produktivního uplatnění lidí (tj. stárnutí, resp. zvýšení počtu obyvatelstva ve vyšším věku, ještě automaticky neznamená, že člověk přestane přispívat do systému a začne z něho čerpat).
Významný je zejména třetí případ. Je chyba v úvaze, že ze skutečnosti zvyšování podílu obyvatelstva ve vyšším věku na celkové populaci se vyvozují neřešitelné problémy penzijního systému.
Tentýž problém je obsažen i v dalším výroku "zmenšující se počet pracovně aktivních lidí bude financovat narůstající počet důchodců".
Úkol:
Proveďte rozbor výroku "zmenšující se počet pracovně aktivních lidí bude financovat narůstající počet důchodců" obdobným způsobem, jakým byl proveden v předcházejícím případě, tj. v případě obdobného výroku "S rychle se rozvíjející stárnoucí populací rostou i náklady na důchody, které budou ukrajovat ze státního rozpočtu stále větší část.".
Následující výrok je závěrem z celé citované pasáže a současně vymezením cíle práce - "stávající důchodový systém (je) neudržitelný v důsledku demografického vývoje". Označme:
* "stávající důchodový systém" - Ds
* "neudržitelný v důsledku demografického vývoje" - Nd
Příslušný výrok můžeme vyjádřit následující můžeme vyjádřit následující binární maticí:
DsNd
0 0
0 1
1 0 Tato
kombinace je v daném výroku neinterpretovatelná.
1 1
Neinterpretovatelnou kombinací zde je případ, kdy by demografický vývoj nebyl příčinou neudržitelnosti stávajícího penzijního systému. To je ovšem rovněž velmi sporné tvrzení. Lze ukázat např. následující významnou interpretaci: Příčinou neudržitelnosti není demografický vývoj, ale selhávání systémů poskytování vzdělání a zdravotní péče, které by umožnily prodloužit období produktivního uplatnění člověka.
Zajímavé je, že autor práce místo aby hledal v řešení, využívá zpochybnitelné tvrzení k tomu, aby se snažil problém představit jako neřešitelný.
Poznámka:
Všimněme si, že pojem a slovo nejsou jedno a totéž. Pojem může být vyjádřen i více slovy. Přitom náš jazyk je velmi tvárný a používá různé odstíny či zabarvení slov. Nicméně v každém textu lze najít nejvýznamnější tvrzení, která se v něm vyskytují, a podrobit je analýze. Při čtení každého textu bychom měli umět nejdůležitější tvrzení nacházet, uvědomovat si, co je považováno za neinterpretovatelné alternativy a zkoušet, zda skutečně interpretaci nemají, či naopak mají. Dobrý text se pozná podle toho, že prezentuje kontexty hlavních tvrzení tak, aby v něm nebyly "vyškrtnuté" (tj. pojmovými určeními vyloučené) alternativy s relevantními interpretacemi.
Navazující příklad viz příloha.
Matice a submatice – jak se rozvíjí naše poznání
Jak jsme si již několikrát řekli, je představa matice, která obsahuje všechna vzájemná určení pojmů, pouze modelem, který jako takový nelze realizovat (vzájemných určení je tak obrovské množství, že nemohou být reálně vytvořena ani v hlavě člověka ani jiným způsobem). Pojmové vyjádření reality si lze představit (a takto modelovat) jako řadu submatic, které z nichž každá je tvořena jen malým zlomkem pojmových určení a jejich interpretací, které však spolu mohou vstupovat do vzájemných interakcí.
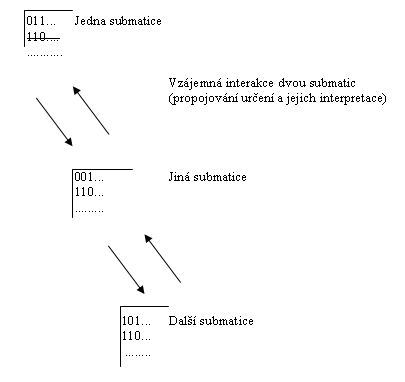
Reakci mezi submatice s našem myšlení si lze představit následujícím způsobem:
* Určení vytvořená a interpretovaná v jedné oblasti jsou převzata do druhé oblasti, propojují se s určením v druhé oblasti.
* Přitom jsou nacházeny interpretace toho, co bylo původně neinterpretovatelné a bylo zdrojem určitosti (tj. ony „vyškrtnuté alternativy“).
* Jakmile jsou takovéto „interpretace neinterpretovatelného“ (v podstatě se jedná o rozpory v našem myšlení, v důsledku nichž dochází ke ztrátě určitosti), odhalovány, měly by být i řešeny, tj. mělo by být pojmy vyjádřeno, za jakých podmínek není dané určení interpretovatelné a kdy se jedná o přesah původního určení.
Poznámka:
Ne každý má schopnost ve své hlavě takto propojovat jednotlivé oblasti poznání a nacházet rozpory v určeních v různých relativně samostatných oblastech svého pojmového vyjádření reality. Prostě takovéto „interpretace neinterpretovatelného“ neodhaluje, nenachází je, nevěnuje jim pozornost, nevyhledává je apod. Bez toho je ovšem pojmové vyjádření reality velmi povrchní a jednotlivá pojmová určení člověk používá jen příležitostně. Jeho názory se vyznačují značnou nekonzistencí, což může oslabit jeho pozici v odborné sféře, v řídící praxi apod.
Schopnost přenášet pojmová určení z jedné oblasti do druhé (z hlediska binárního maticového modelu se jedná o interakci dvou submatic), odhalovat a řešit rozpory v pojmových určeních, které přitom vznikají, si je nutné vycvičit. Z hlediska poznávání reality a jeho vyjádření v pojmech (tj. z hlediska sdělitelného poznávání reality) je to ovšem velmi důležité.
Úkol:
* Udělejte binární matici pro dva pojmy.
* Přeškrtnutím označte některé řádky jako neinterpretovatelné, přitom tak, aby to odpovídalo realitě.
* Slovně vyjádřete, co váš zápis znamená.
Úkol:
Totéž udělejte pro případ tří pojmů.
Úkol:
Vyjádřete pomocí binární matice následující určení:
* "Ekonomie je věda."
* "Lidské schopnosti mohou být též kapitálem."
* "Když prší, rostou houby, když neprší, houby nerostou."
Úkol: Napište na papír hlavní body této části a teprve poté se podívejte na její shrnutí.
Úkol: Pokuste se zformulovat nejméně tři otázky, které ve Vás vyvolala tato část, a zašlete je na adresu obou vedoucích kurzu - labe@mnet.cz; valencik@cbox.cz.